Why we should be trying to do better than Corsi and Fenwick
May 28, 2014
I think Corsi and Fenwick suck. I think this not because I’m an old-school, Brian Burke-ian stats hater. When it comes to “advanced” hockey stats, the formula shots + blocks + misses = corsi is lazy and oversimplistic. I think they suck because (at best) they’re weak proxies for what we believe is important in a hockey game (puck possession). I think they suck because I know we can do better.
I mostly dislike them because they’re a constant reminder of the fact that there’s so little investment in hockey analytics by teams and by the media. Don’t get me wrong, there’s fantastic work being done by lots of people on the blogosphere, but until NHL invests in player tracking technology (and hopefully makes it publicly available) we’re going to be stuck using weak proxies like Fenwick and Corsi to measure possession.
In this post I don’t intend to bring you to my side. You probably clicked on this post precisely because you know what Fenwick and Corsi are and find them valuable. I agree with you on that. They’re infinitely better than plus/minus and other run-of-the-mill stats. But until we get player-tracking data and other more sophisticated stats, I think it’s important that we understand how to properly use Corsi and Fenwick.
The point of this post is to convince you that Corsi and Fenwick don’t do a particularly good job of predicting who will win hockey games, and they aren’t any better at this task than the traditional shots-on-goal statistic. I also hope to build our understanding of the types of questions that Corsi and Fenwick can answer and when it’s appropriate to use them to build narratives about games. Right now I’m mostly concerned with team-Corsi and team-Fenwick, not individual player Corsi/Fenwick, but in the future I’ll hopefully dive into the value of C/F on assessing player performance.
Corsi, Fenwick, shots, and goals
This post builds on my previous blog post, Why popular advanced stats are bad at predicting who wins. In that article, I show that when the score is tied at some point in the game, the team that has a higher Corsi or Fenwick for the rest of the game is more likely to lose than win. Many rightly pointed out that this doesn’t fully account for scoring effects, although that should be less of a problem when I look games that are tied with just a couple minutes remaining.
What I’m going to do in this post is evaluate how well previous shot attempts (rather than future, as before) predict the team who wins. To analyze the predictive power of Corsi and Fenwick (C/F), I’m using the play-by-play data from every NHL regular season game from 2005-2006 through 2013-2014. This gives us data from over 10,000 games to play with.
The quantity that I’m going to consider throughout the article is how well stats like C/F correlate with winning the hockey game. Specifically I’m answering the question, what percentage of teams that lead in Corsi/Fenwick/shots-on-goal/goals at each second of regulation win the game?
Quick crash course for anybody not familiar… Shots-on-goal (SOG) are shots that either go into the net or are saved by the goaltender. Fenwick for a team is equal to SOG plus shots that go wide or high are aren’t defended by the goalie. Corsi equals Fenwick plus shots that are blocked by a defender.Usually we’re interested in either Corsi/Fenwick differential (team A’s C/F minus team B’s C/F) or Corsi/Fenwick percent (team A’s C/F divided by team B’s C/F).
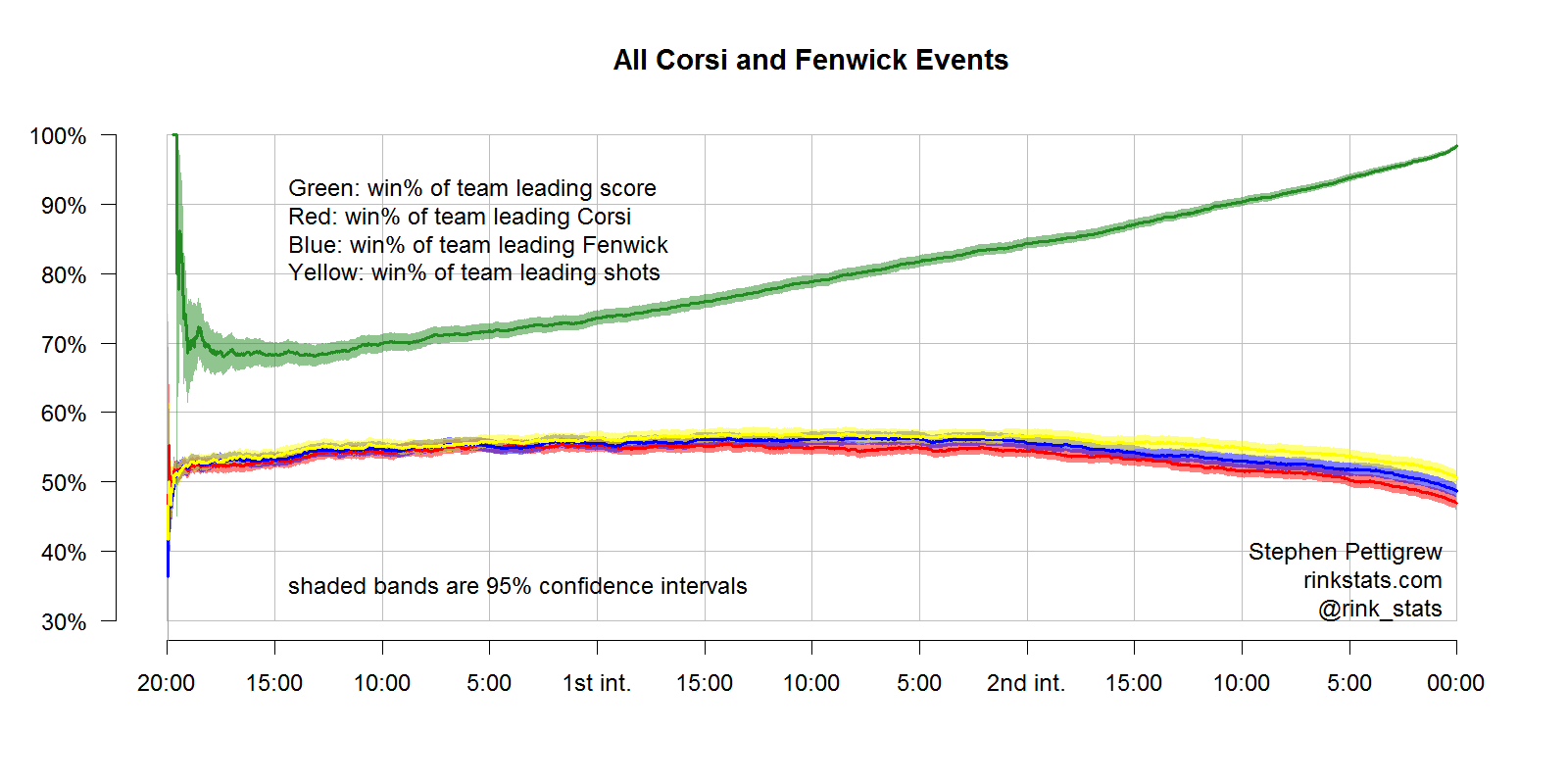
The graph above shows the winning percentage for the team that’s ahead in each of these four statistics at each of the 3,600 seconds of regulation. In other words, the solid green line is the percentage of teams with a lead, at that point in the game, who end up winning the game. Yellow is the team with more shots, and red and blue are the team leading Corsi and Fenwick, respectively. The team “leading” in Corsi or Fenwick is the one with a higher number of C/F events or the one with a Corsi% or Fenwick% greater than 50%. The shaded bands around each of the four lines are 95% confidence intervals.
As you can see, all three shooting statistics are drastically outperformed by the score differential, in terms of how well they predict who will win the game. What this tells us is that at any given point in the game, if you’re told which team is leading in the score and in Corsi or Fenwick and you’re asked to bet who will in the game, you’ll win that bet between 15 or 50 percentage points more often if you pick the team leading the score.
This seems obvious. Clearly how many shots you attempt is much less important than the number of shots that hit the back of the net. Also, most hockey stats folks will notice that I’ve included special teams shots and shots that occur when the game isn’t close. I’ll account for these two things now.
Even strength Corsi/Fenwick
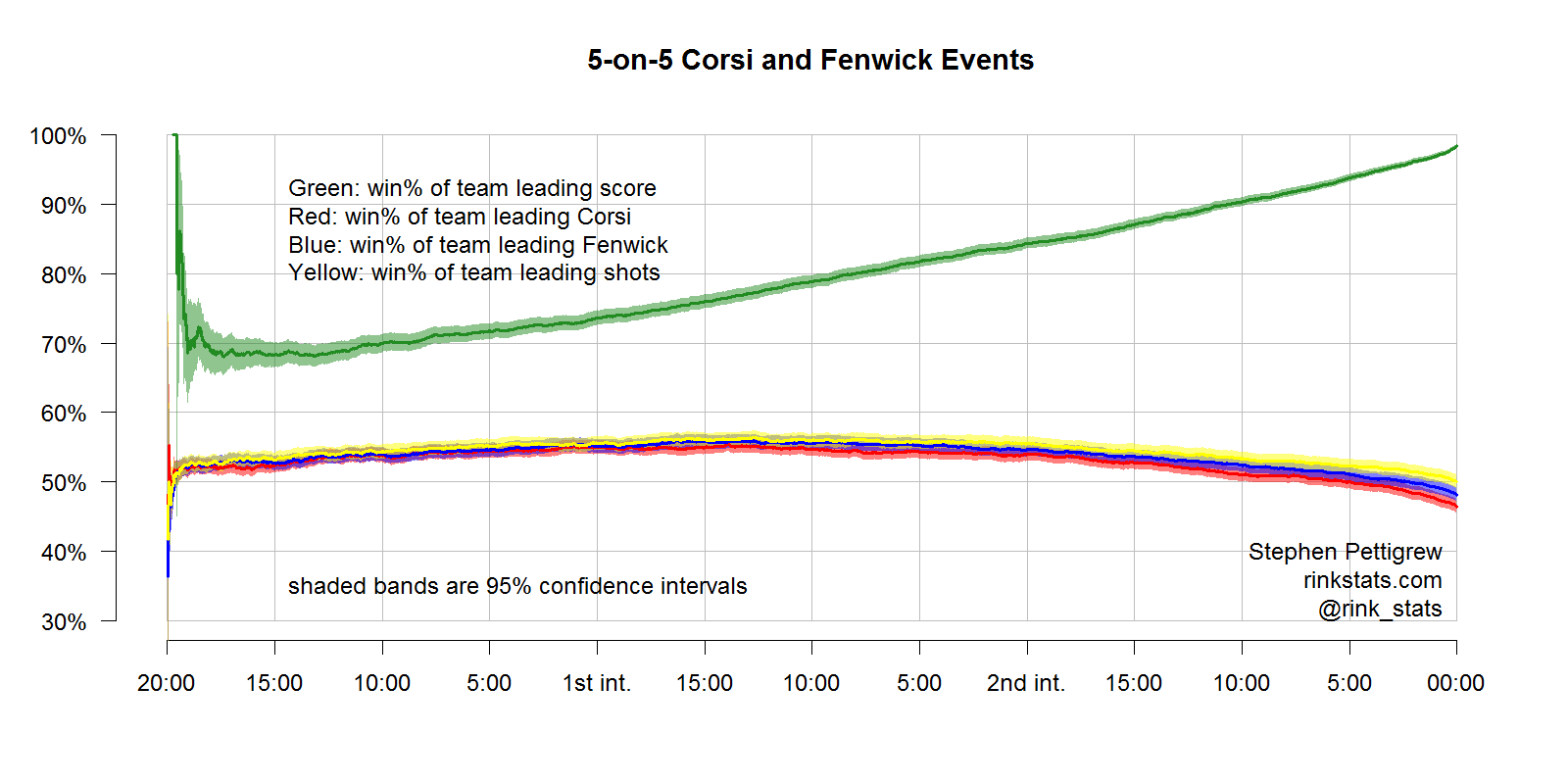
The graph above is the same as the one before, except I’ve only kept events that occurred during a 5-on-5 when I calculated Corsi, Fenwick, and shots. You can see that this graph looks extremely similar to the first one. It’s tough to see, but Corsi and Fenwick actually have slighly worse predictive power when you restrict the analysis to 5-on-5, compared to when you don’t. This makes a lot of sense, since a teams with more powerplay opportunities is likely to have a higher C/F percent or differential, and they’re also likely to get more powerplay goals and thus more likely to win the game.
What’s interesting to note is the upsidedown U shape to the red, blue, and yellow curves. The fact that these curves begin to diminish in predictive power is direct evidence of the importance of scoring effects on these statistics. The downturn in the curves seems to begin around the beginning of the 3rd period. This is when a team trailing on the scoreboard will start throwing more pucks at the net in hopes of getting a lucky bounce.
Corsi/Fenwick-close
To account for this fact, hockey analytics folks use the Corsi-close and Fenwick-close statistics. The intuition behind them is that we can mitigate the scoring effect by only looking at shot attempts that occur when the score is close. So what is a “close” score? There doesn’t seem to be a consensus answer to this, and different websites use different score thresholds to define close. Usually, though, close is either within 2 goals, 1 goal, or tied. I’ll consider each of these tresholds.
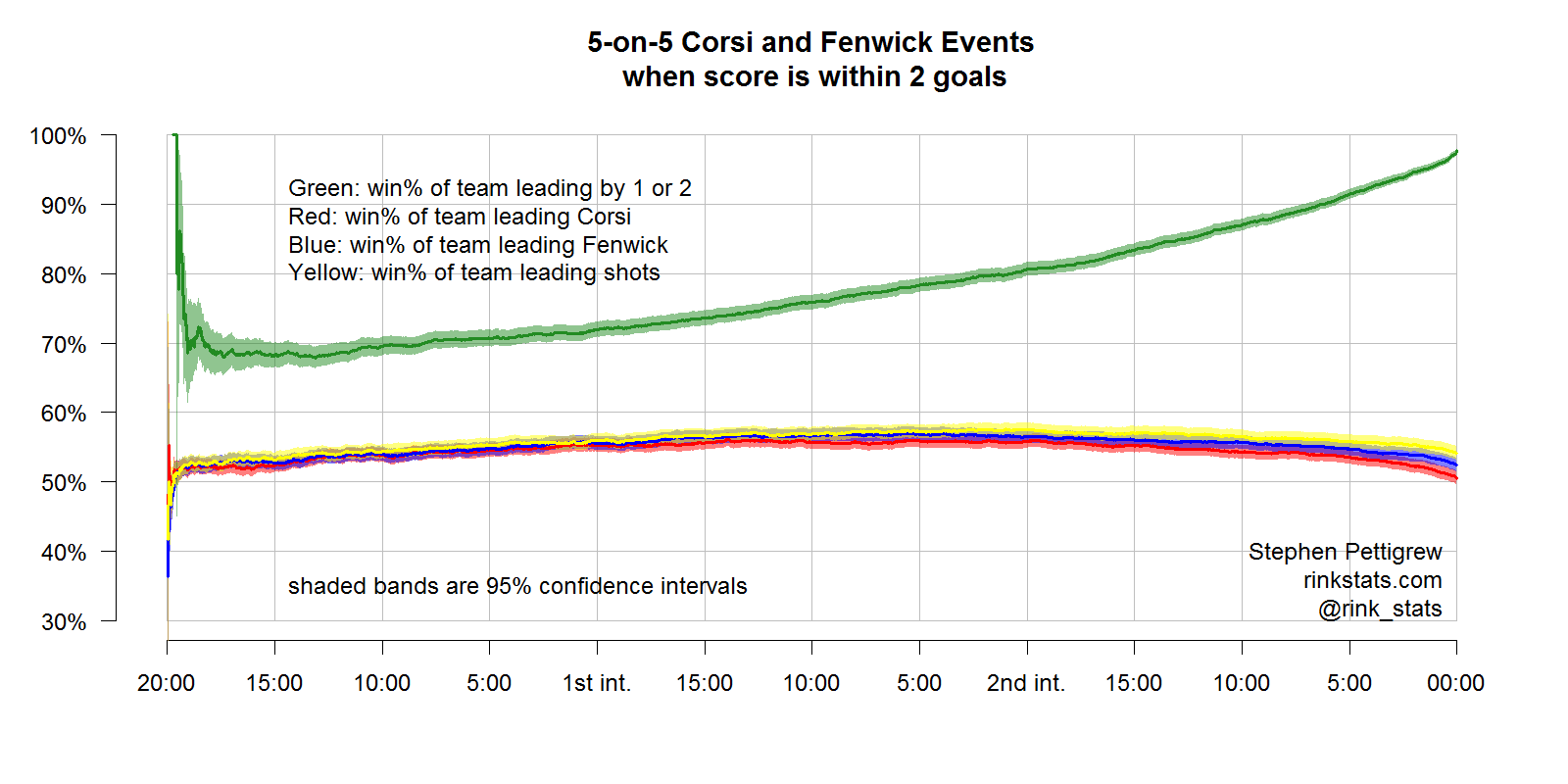
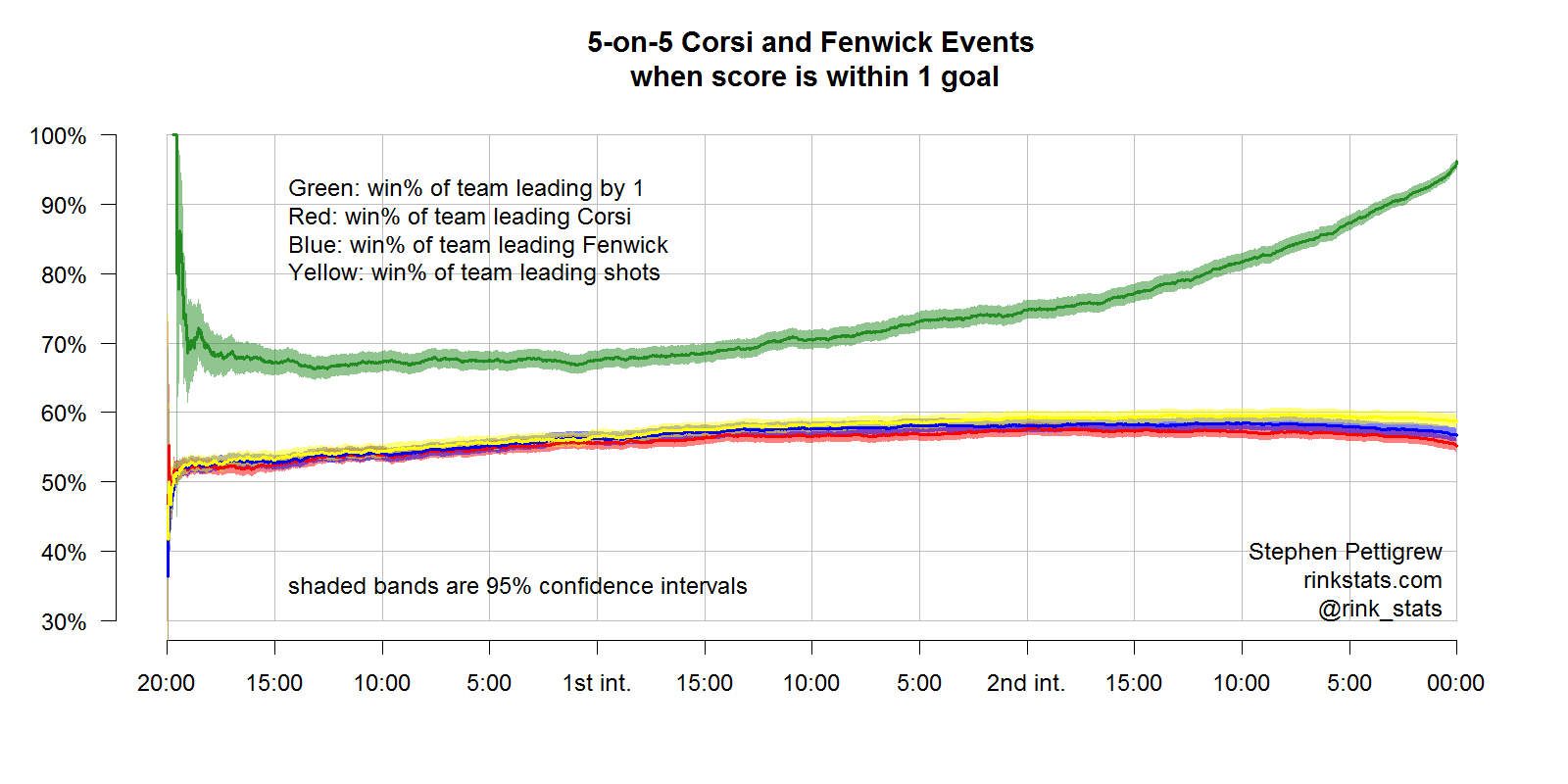
The two graphs above show the predictive power of Corsi and Fenwick when the score is within two goals and within one. In both cases, the predictive power of the statistics has improved from where it was before accounting for the score, but C/F are still being strongly outperformed by the actual score.
It’s also interesting to note than in both of these graphs, as well as the earlier ones, the shooting stat with the highest predictive power of winning is shots on goal. This is partly because SOG includes goals, which determines who wins the game. But this trend of SOG outperforming Corsi and Fenwick persists even when we look at only the SOG that were not goals.
Unfortunately score effects are still very evident in these C/F-close statistics, which were meant to account for them. When the score is within 2 goals, you begin to see the downward trend in the predictive power of C/F about 5 minutes into the third period. When the score is within one goal, the downward slide doesn’t begin until there’s 5 minutes left in regulation.
In each of the graphs above, the stat that’s most informative is the actual score differential. While the Corsi-close and Fenwick-close leaders win the game less than 60% of the time, the team with a 1 or 2 goal lead wins at least 65% of the time. But what happens when the score is tied, and you don’t have this luxury of picking the team that’s already ahead?
Corsi/Fenwick-tied
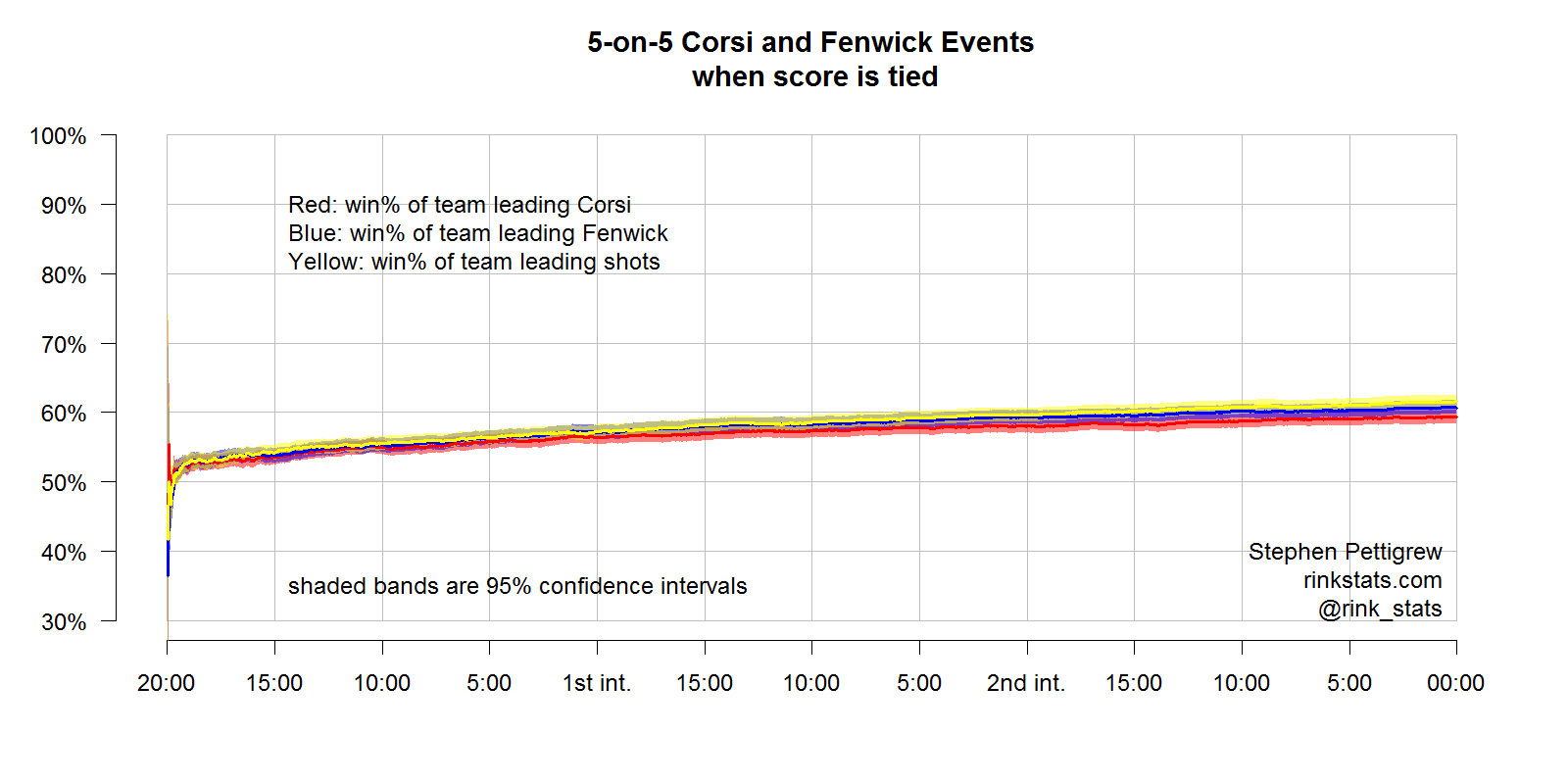
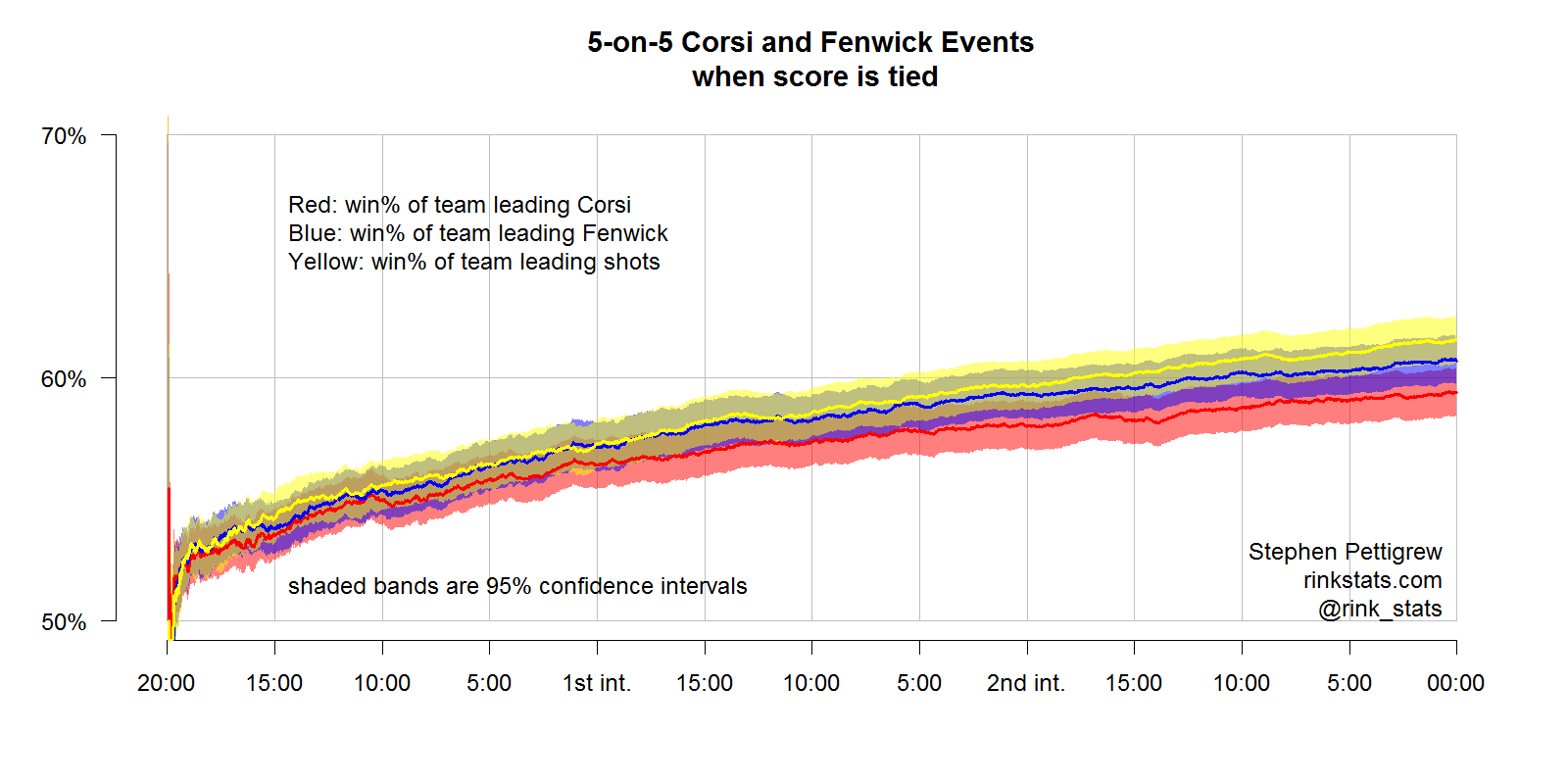
The graph above (as well as the zoomed-in version) shows the predictive power of full-strength Corsi, Fenwick, and shots-on-goal that occur during tied games. We can clearly see that the upsidedown U shape, characteristic of scoring effects, has disappeared in this graph. All three of these statistics get better in their predictive power as the game goes on.
In games that are tied at the first intermission, the team leading in Corsi-tied, 5-on-5 wins the game 56.43% of the time (plus or minus 1.00%). The team leading Fenwick-tied, 5-on-5 wins 57.13% (+/- 1.00%). The team with more shots on goal wins 57.28% (+/- 1.02%).
In games tied at the second intermission, the team leading in Corsi wins 59.03% of games (+/- 0.99%). The team leading Fenwick wins 59.31% of the time (+/- 0.998). And the team leading in SOG wins 59.66% of those tied games (1.00%).
What should be most concerning to Corsi and Fenwick lovers is that neither statistic has better predictive power than shots-on-goal differential. In fact as the game goes on, SOG actually seems to get better at predicting winners than C/F, although it’s still within their confidence intervals.
Takeaways
So what does all this tell us about the value of Corsi and Fenwick in determining which team is likely to win a game? First, in games that are not tied, shooting and possession statistics have little value when compared to actually looking at the score. In games that are tied, using C/F-tied to predict the winner will do better than a 50-50 coin flip, but your odds of a correct prediction aren’t overwhelming (about 60%).
Also important is the fact that score effects persist in C/F-close statistics, when “close” is defined as anything except a tied game. This suggests that the only version of these statistics with enough predictive power to justify being used is Corsi-tied or Fenwick-tied, although both are outperformed by shots-on-goal-tied.
Despite their drawbacks, though, Corsi and Fenwick do still have value. When you look at the graph of each team’s Corsi or Fenwick throughout a game, you can identify time periods where teams are taking lots of shots or very few.
Where you have to be careful is in drawing too many conclusions about what these droughts mean. A team that’s going through a shot drought might be working the clock and maintaining good possession, just not taking shots. Or they could be stuck in their defensive zone for long stretches, without puck possession.
This gets to what should be the broader takeaway from this article. Given that Corsi and Fenwick don’t have much more predictive power than SOG, we have to ask what value they’re actually adding. In a theoretical sense, Corsi and Fenwick are better than SOG since they serve as a proxy measure of how much time each team had the puck.
But when the NHL implements player and puck tracking technology into their arenas, as has been rumored, it will no longer be necessary to use Corsi or Fenwick as proxy measures of possession. Assuming the data become publicly available, we’ll be able to directly calculate the amount of time each team had the puck in their zone, or how much time they possessed the puck.
Clearly, I haven’t discussed the value of Corsi and Fenwick as player-level statistics. That’s a next step, although I suspect that player-tracking technology will open up new doors to great new metrics that render Corsi and Fenwick obsolete. For now though, my intuition is that Corsi and Fenwick will outperform SOG when evaluating players. This is partly because the number of SOG is necessarily smaller than Corsi or Fenwick and thus SOG-differential has less variability between players. Unless missed and blocked shots are complete statistical noise, we should be able to leverage the added variability in Corsi or Fenwick to evaluate players. But, again, that’s next step.

