Why the NHL's new conference alignment is unfair for Eastern teams
July 21, 2013
On Friday the NHL released the 2013-2014 regular season schedule. This season will be the first played under the new conference and division alignment which sent Winnipeg west and Columbus and Detroit east. A key aspect of the new alignment is that there is an imbalance in the number of teams in the East (16) and in the West (14). In this post I’ll discuss a paper I wrote a couple months back (How the West will be Won: Using Monte Carlo Simulations to Estimate the Effects of NHL Realignment). In the paper, I show that because 8 teams make the playoffs from each conference, the new alignment and playoff qualification rules unfairly disadvantage Eastern Conference teams.
Specifically, I’ll show that the 8th seed in the East will (on average) be 2 or 3 points better in the standings than the 8th seed in the West. And I’ll show that about 40% of the time, the 9th seed in the East would have made the playoffs if they were in the West (compared to just 20% of the time when the inverse is true).
This research was my first foray into hockey analytics. Back in March the NHL announced it had settled on a plan to realign the conference and division structure. Starting this upcoming season, the NHL will have two conferences, and each conference will feature two divisions. The Eastern Conference will have 16 teams, and the Western Conference will have 14 teams. Each conference will continue to feature an 8 team playoff, with the conference winners meeting in the Stanley Cup Final.
It was this final feature of the realignment that caught my attention. How is it that the NHL owners (especially in the East) agreed to a plan in which Eastern teams have a 50% chance of making the playoffs, compared 57% among Western teams? Almost automatically, it has become harder to qualify in the East than in the West. So this got me thinking about how this new alignment will actually play out and whether or not it will actually be unfair. I was specifically interested in what I call in the paper the “conference gap,” which is the number of end-of-season points by the 8th seed in the East minus the points by the 8th seed in the West.
The obvious problem with learning about the conference gap is that the NHL hasn’t yet played a single game under these new rules, let alone a whole season. So, being a good statistician who knows how to write fancy R code, I decided to simulate full NHL seasons and then calculate the conference gap. And not just 5 or 10 simulated seasons. I simulated 10,000 of them.
The intuition behind my simulation was pretty straightforward. To simulate one season, I randomly draw 30 numeric values from a normal (bell-shaped) distribution. These 30 values correspond to the underlying quality or ability of the 30 teams. Then I go through and simulate all 1,230 games in the NHL schedule (adjusted appropriately to take into account the new scheduling matrix). For each game, I draw a number from two normal distributions (each centered at the value of two teams’ underlying ability). These two numbers can be thought of the amount of effort or skill the two teams put forth during this game. The game is “won” by whichever team drew the higher number for their game performance value. I also account for games going into overtime, which I discuss this more thoroughly on page 12 of the paper.
After I’ve simulated all 1,230 games, I calculate the final standings as well as the conference gap. Then as a point of comparison, I use the same 30 underlying ability values to rerun the season, only this time I apply the old schedule matrix, old alignment, and old playoff qualification rules. I repeat all these steps 10,000 times (essentially simulating 10,000 seasons) to get a nice understanding of how big the conference gap will be. In the paper, I go into more detail about how I tweaked my algorithm, so that I don’t end up with the best team having 150 points and the worst having 15. That discussion starts on page 16 of the paper. It suffices to say though that you’d have a pretty tough time telling the difference between results from my simulations and the results from a real NHL season.
The graph below plots the conference gap for the 10,000 seasons simulated under the old and new alignment structures. The blue parts of the graph correspond with the new rules, and the red parts correspond with the old.
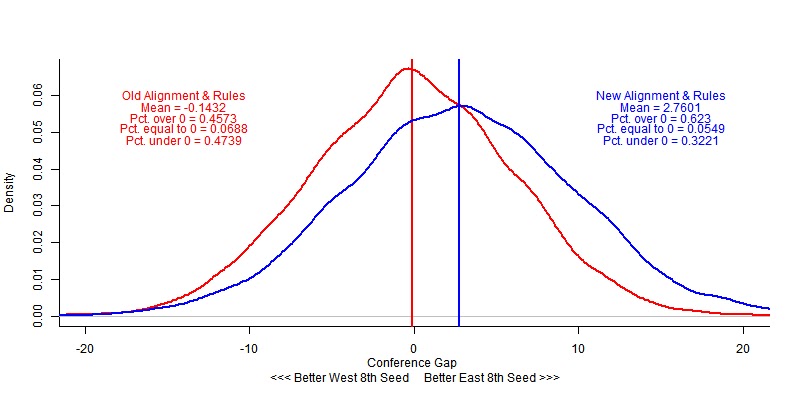
What you can see is that under the old rules the average conference gap was 0.143 points in favor of the Western Conference, although this value is not statistically significantly different from zero. Under the new rules, however, the average conference gap is 2.76 points. This means that, on average, the 8th seed in the East had 2.76 more points than the 8th seed in the West.
The graphs also contain the information of how often the conference gap favored the East versus the West. In the old alignment, 47% of seasons had the better 8th seed in the West, and 46% of seasons had an better Eastern 8th. In the new alignment, this difference gets huge. 62% of the time, the East’s 8 had a better record than the West’s 8, compared to just 32% of the time the inverse was true. This means that starting next year, we’re about twice as likely to see a better Eastern 8th. Under a fair set of rules in which your geographic location shouldn’t affect your chances of making the playoffs, these numbers should be 50/50.
My simulations also show that 38% of the time, the 9th seed in the East would have qualified for the playoffs if they had only been located in the West. The opposite, in which the 9th Western team would have made the playoffs in the East, occurs only 21% of the time. Even more striking, my simulations suggest that 21% of the time the 10th (!) seed in the East would make the playoffs if they were in the Western Conference.
I might do another post in the next couple days, detailing a couple other interesting things that are in the paper. But until then, here’s the takeaway… Expect that in about 62% of seasons, the 8th seed in the East will have a better record than the 8th seed in the West. And in 38% of seasons, the 9th seed in the East will have a better record than the 8th seed in the West. And

